"... μπορούμε, με μια πολύ όμορφη τεχνική, να φέρουμε όλες αυτές τις πόλεις
και τις πληροφορίες για τις μεταξύ τους αποστάσεις σε μια και μόνο,
δισδιάστατη εικόνα. Αυτό όμως θα το δούμε στο επόμενο κείμενο, πολύ
σύντομα!"
Κάθε φορά που προσπαθείς να βάλεις τα πράγματα σε μια σειρά, ο θεός (και συγγραφέας του "Απο την τάξη στο χάος κι εμπλοκή: Πώς να δημιουργήσετε το δικό σας σύμπαν σε 3.1415928 απλά βήματα" εκδόσεις Έρεβος), απελευθερώνει μια πιρουνοβόμβα στο δικό σου μικρό προσωπικό σύμπαν και σε κάνει να νιώθεις σα να προσπαθείς να τρέξεις τα 100 μέτρα σε 8 δευτερόλεπτα βυθισμένος σε μια πισίνα γεμάτη μέλι.
Αυτός ίσως να είναι ένας πιο περίπλοκος τρόπος για να περιγράψω τι έχει συμβεί μέσα σε αυτές τις 40 ημέρες απο το προηγούμενο κείμενο και το πώς είναι δυνατόν αυτό το διάστημα να χαρακτηριστεί "πολύ σύντομα!", αλλά πιστέψτε με, βλέποντας τα πράγματα απο τη δική μου σκοπιά, η παραπάνω εξήγηση φαντάζει απίστευτα λογική! Όπως είχε πεί και ο Προμηθέας της υπέρτατης γνώσης (γνωστός και ως Murphy) "Αν ξέρεις οτι κάτι μπορεί να πάει "στραβά" (ή τέλος πάντων, λιγότερο ευνοϊκά) και δεν προετοιμαστείς για αυτό....Τότε αυτό θα πάει στράβα (έστω και αν η πιθανότητα για αυτό το ενδεχόμενο φαινόταν πάρα πολύ μικρή)"....Αυτός...ξέρει!
Οπότε, ας δούμε λίγο πιο αναλυτικά αυτές τις δύο, φαινομενικά αθώες γραμμές της εισαγωγής, πρίν κάποιο ενδεχόμενο με πιθανότητα τόσο μικρή που δεν χωράει σε ανθρώπινο κεφάλι, αποφασίσει να καθυστερήσει αυτή τη σειρά πόστ για άλλη μια φορά (!).
Σύμφωνα λοιπόν με τα δεδομένα της Economist Intelligence Unit, οι δύο πόλεις στις οποίες ο τρόπος διαβίωσης απέχει τη "μεγαλύτερη απόσταση", είναι το Karachi - Pakistan και το Vancouver - Canada.
Εδώ βέβαια, δεν αναφερόμαστε στη γεωγραφική απόσταση, αλλά στην απόσταση όπως αυτή ορίζεται απο το διάνυσμα των 40 δεικτών που χαρακτηρίζουν κάθε πόλη. Αυτή η έννοια της απόστασης, έχει μια ιδιαίτερη σημασία και περιεχόμενο.
Για να δούμε λοιπόν: Τι πληροφορίες μπορεί να μας δώσει η έννοια της απόστασης; Ποιό είναι το μονοπάτι της "ελάχιστης προσπάθειας", ώστε το Karachi να "μετατραπεί" σε Vancouver; Ποιό είναι το μονοπάτι των λιγότερων μεταρυθμίσεων για τον ίδιο σκοπό; Ποιά είναι τα παραπάνω μονοπάτια όσο αφορά την Αθήνα;
Το κλειδί των απαντήσεων στις παραπάνω ερωτήσεις, βρίσκεται κατα ένα μεγάλο μέρος, στην έννοια της "απόστασης". Ήδη στο προηγούμενο κείμενο, είδαμε την έννοια της γνώριμης Ευκλείδιας απόστασης ανάμεσα στα σημεία ενός χώρου. Η μόνη διαφορά στη περίπτωση των δεδομένων της EIU και την "απόσταση" ανάμεσα σε δύο σημεία (για παράδειγμα, ανάμεσα στην Αθήνα και τη Θεσσαλονίκη) είναι οτι αυτός ο χώρος δεν έχει 3 αλλά 40 διαστάσεις.
Ένα χώρο 40 διαστάσεων, είναι ίσως δύσκολο να τον φανταστεί κανείς. Με τι μοιάζει ένα σπίτι στις 40 διαστάσεις; Με τι μοιάζει ένα αυτοκίνητο; Ένα ποτήρι, ή ένας απλός κύβος (ένα παραδοσιακά τρισδιάστατο σχήμα); Τι είναι διάσταση;
Διάσταση είναι μια ιδιότητα ενός αντικειμένου που αν τη στερηθεί, τότε δεν μπορεί να οριστεί πλήρως. Είναι αδύνατον να οριστεί ένας κύβος (ένα στερεό 3 διαστάσεων: Μήκος, Ύψος, Βάθος) στις 2 διαστάσεις γιατί θα ήταν αδύνατον να εκφραστεί το βάθος του.
Η απεικόνιση ενός πολυδιάστατου χώρου είναι απο τις λίγες περιπτώσεις όπου χρειάζεται να "δούμε" ακριβώς τη μορφή αυτού του χώρου. Συνήθως, τον δουλεύουμε "στα τυφλά" με βάση κάποιους απλούς κανόνες. Για παράδειγμα, με βάση τον απλό κανόνα: "Δύο διανύσματα είναι κάθετα όταν το εσωτερικό γινόμενο τους είναι 0", μπορούμε να κατασκευάσουμε κάθετα διανύσματα στις οποιεσδήποτε Ν διαστάσεις ΧΩΡΙΣ να χρειάζεται να τις "δούμε".....Δεν είναι ανάγκη να το "δείς" για να πιστείς (!) (Για περισσότερες λεπτομέρειες και μια ωραία εισαγωγή στο θέμα τουλάχιστον για τις 4 διαστάσεις μπορείτε να δείτε εδώ)
Δυστυχώς, δεν θα κατανοήσουμε ποτέ την μαγεία ενός "τετραπλού τόλουπ" στις 6 διαστάσεις (ο Κωστάλας παραμένει αδιάβλητος σε μετασχηματισμούς (!)), ή τι αδιανόητα αεροβατικά μπορεί να σκεφτεί ο πιλότος των 9 διαστάσεων. Δεν είμαστε φτιαγμένοι για αυτούς τους χώρους. Οι αισθήσεις μας είναι περιορισμένες στις 3 (το πολύ) διαστάσεις.
Στη προσπάθεια μας λοιπόν να κατανοήσουμε ένα 40διάστατο αντικείμενο στα περιθώρια ενός δισδιάστατου χώρου (ενός φύλου χαρτιού δηλαδή) και γνωρίζοντας πως δεν μπορούμε να του στερήσουμε καμία διάσταση τι κάνουμε;
Μπορεί να μην μπορούμε να στερήσουμε μια διάσταση απο τον κύβο, αλλά μπορούμε να βρούμε ένα τρόπο ώστε η τρίτη διάσταση να εκφραστεί μέσα απο τις δύο...Μπορούμε δηλαδή να προβάλουμε τις 3 διαστάσεις σε 2 ή γενικότερα, τις πολλές διαστάσεις σε λίγες...με την προυπόθεση βέβαια οτι αποδεχόμαστε κάποιο σφάλμα....Τι είναι αυτό το σφάλμα; Για να δούμε...
Στη παρακάτω εικόνα, ποιό σχήμα είναι ένα πραγματικό εξάγωνο και ποιό σχήμα είναι ένας κύβος καθώς τον κοιτάμε απο μια γωνία του;
Ακριβώς αυτό....Προσπαθόντας να προβάλουμε ένα κύβο απο τις τρείς στις δύο διαστάσεις, παραμορφώθηκε τόσο πολύ, που κατάντησε ένα τιποτένιο δισδιάστατο 6γωνο.....Απ' τα ανώγια, στα κατώγια...
Η προβολή των 3 διαστάσεων στις 2 είναι υπόθεση εύκολη...κυρίως επειδή τα μάτια και ο εγκέφαλος μας, είναι φτιαγμένα για να καταλαβαίνουμε δισδιάστατα αντικείμενα και να "φανταζόμαστε" τα τρισδιάστατα. Πώς όμως θα προβάλουμε 40 διαστάσεις; Δεν είναι μια δεν είναι δύο, δεν είναι τρείς....Είναι 40!
Είτε στη μια, είτε στις δύο, είτε στις τρείς, είτε στις δεκατρείς διαστάσεις, η έννοια της απόστασης* παραμένει η ίδια. Δέκα μέτρα απόσταση στις 20 διαστάσεις είναι ακριβώς δέκα μέτρα και στις 2 διαστάσεις. Και η απόσταση, είναι απλά ένας θετικός (πάντα) αριθμός.
Για να δούμε λοιπόν, μπορούμε να φανταστούμε ένα τρόπο, ώστε να προβάλουμε τα σημεία ενός 40διάστατου αντικειμένου στις 2 διαστάσεις με όσο το δυνατόν μικρότερη παραμόρφωση;
Η απάντηση σε αυτή την ερώτηση είναι σχετική με το αντικείμενο του διαγωνισμού Best City Contest. Ο διαγωνισμός μάλιστα, μας καλεί να προβάλουμε τις 40 διαστάσεις (ή υποσύνολο αυτών, ή ακόμα και νέο σύνολο με την προσθήκη άλλων δεικτών) σε 1. Να κατατάξουμε δηλαδή τις πόλεις επάνω σε μια γραμμή.
Αυτό μπορούμε να το κάνουμε με πάρα πολλούς τρόπους. Ένας απο αυτούς είναι η τεχνική του Multidimensional Scaling. Η τεχνική αυτή λύνει την εξής ωραία σπαζοκεφαλιά: Γνωρίζοντας μόνο τις αποστάσεις ανάμεσα σε ένα σύνολο απο σημεία σε κάποιο χώρο (Μ διαστάσεων), μπορείς να βρείς τη σχετική θέση των σημείων αυτών σε ένα άλλο χώρο (Ν διαστάσεων, Ν<=Μ), έστω και με κάποιο μικρό (κατα προτίμηση) σφάλμα;
Δεν μας ενδιαφέρει δηλαδή το πώς ακριβώς είναι τοποθετημένα αυτά τα σημεία πραγματικά στον 40διάστατο χώρο τους, αν δημιουργηθεί μια δισδιάστατη απεικόνιση που διατηρεί τις σχετικές αποστάσεις των σημείων τότε αντικρίζουμε ένα (απλό) χάρτη αυτού του (σύνθετου) πολυ-διάστατου τοπίου.
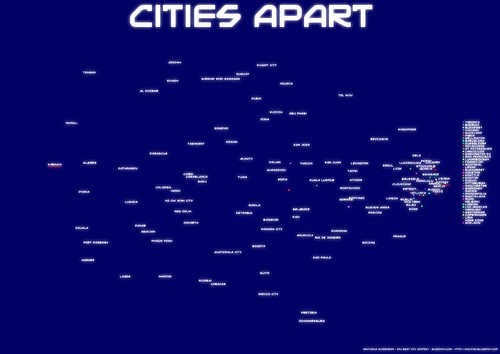
Να ένας "απλός" χάρτης:
Η παραπάνω εικόνα αποτελέι τη "λύση" της προβολής των 40 διαστάσεων σε 2 με τη μέθοδο του Multidimensional Scaling. Εδώ αξίζει να σημειωθεί οτι επειδή το πρόβλημα του ακριβούς ταιριάσματος των αποστάσεων ανάμεσα σε κάθε ζεύγος σημείων μπορεί να είναι αρκετά δύσκολο (ανάλογα με την εφαρμογή), μια υποκατηγορία μεθόδων του Multidimensional Scaling προσπαθεί απλά να "ταιριάξει" την κατάταξη των αποστάσεων παρά τις απόλυτες τιμές τους (Όπου εδώ η "κατάταξη" είναι η σειρά με την οποία εμφανίζονται οι πόλεις στα διαγράμματα του προηγούμενου κειμένου). Μια τέτοια μέθοδος έχει χρησιμοποιηθεί και για τη δημιουργία αυτού του χάρτη.
Μια πρώτη παρατήρηση είναι οτι οι πόλεις που ανήκουν σε εύρωστες οικονομικά χώρες (όπως η Ευρώπη, ο Καναδάς και η Αμερική) βρίσκονται όλες μαζί σε μια κοντινή γειτονιά ενώ οι πόλεις που βρίσκονται σε λιγότερο εύρωστες χώρες είναι πιο αραιά τοποθετημένες. Αυτό σημαίνει οτι ο τρόπος ζωής σε αυτές τις περιοχές έχει χαρακτηριστεί απο τους δείκτες και τη βαθμολόγηση της EIU, ώς περίπου ίδιος. Απο εκεί και περά όμως, οι υπόλοιπες πόλεις είναι λιγότερο προβλέψιμες και μπορεί να υπερτερούν σε μια μικρή ομάδα δεικτών αλλά να υστερούν σε κάποια άλλη.
Στο μεταξύ, γράφοντας κομμάτια αυτού του κειμένου, έληξε και η προθεσμία υποβολής συμμετοχών στον διαγωνισμό Best City Contest και είναι πλεόν δυνατόν να δούμε και την πολύ ενδιαφέρουσα δουλειά που έχει γίνει και απο άλλους χρήστες.
Έτσι λοιπόν, ένα παρόμοιο χάρτη στον οποίο είναι ακόμα πιο προφανής αυτή η διαίρεση δημιούργησε ο Alexander Kosenkov για τον διαγωνισμό και μπορείτε να τον δείτε στο BuzzData.
Η δημιουργία αυτού του χάρτη κάνει λίγο πιο προφανή πια και τα υπόλοιπα ερωτήματα, όπως: Πώς θα μπορούσε το Karachi να γίνει Vancouver; (και πόσο γρήγορα;) Ποιός είναι ο δρόμος της μικρότερης προσπάθειας ώστε με μικρούς μετασχηματισμούς ο τρόπος ζωής σε μια πόλη να προχωρήσει πρός αυτόν μιας άλλης πόλης;
Μικρές υποθέσεις και δοκιμές για τις απαντήσεις στις παραπάνω ερωτήσεις, με έκαναν να συμμετέχω τελικά και εγώ στον διαγωνισμό με ότι μπορούσα να καταφέρω στον διαθέσιμο ελεύθερο χρόνο και πάντα δουλεύοντας με την έννοια της απόστασης και προσπαθόντας να δημιουργήσω μια αντικειμενική κατάταξη (αντί για μια υποκειμενική που θα ήταν βασισμένη σε κάποια αυθαίρετη (ή και δικαιολογημένη) επιλογή δεικτών).
Οι ανυπόμονοι μπορείτε να ρίξετε μια ματιά στη συμμετοχή στο PDF που υπάρχει αναρτημένο στο BuzzData αν και σκοπεύω να γράψω μερικά ακόμα λόγια για τη συμμετοχή σύντ.........
Κάποια στιγμή στο μέλλον!
Σημειώσεις:
*: Η έννοια της απόστασης παραμένει η ίδια όταν ο χώρος συμμορφώνεται με την Ευκλείδια γεωμετρία....Υπάρχουν και γεωμετρίες στις οποίες η συντομότερη απόσταση ΔΕΝ είναι η ευθεία....Γίνεται, γίνεται....Θυμίσου, δεν είναι ανάγκη να το "δείς" για να "πειστείς"...
Κάθε φορά που προσπαθείς να βάλεις τα πράγματα σε μια σειρά, ο θεός (και συγγραφέας του "Απο την τάξη στο χάος κι εμπλοκή: Πώς να δημιουργήσετε το δικό σας σύμπαν σε 3.1415928 απλά βήματα" εκδόσεις Έρεβος), απελευθερώνει μια πιρουνοβόμβα στο δικό σου μικρό προσωπικό σύμπαν και σε κάνει να νιώθεις σα να προσπαθείς να τρέξεις τα 100 μέτρα σε 8 δευτερόλεπτα βυθισμένος σε μια πισίνα γεμάτη μέλι.
Αυτός ίσως να είναι ένας πιο περίπλοκος τρόπος για να περιγράψω τι έχει συμβεί μέσα σε αυτές τις 40 ημέρες απο το προηγούμενο κείμενο και το πώς είναι δυνατόν αυτό το διάστημα να χαρακτηριστεί "πολύ σύντομα!", αλλά πιστέψτε με, βλέποντας τα πράγματα απο τη δική μου σκοπιά, η παραπάνω εξήγηση φαντάζει απίστευτα λογική! Όπως είχε πεί και ο Προμηθέας της υπέρτατης γνώσης (γνωστός και ως Murphy) "Αν ξέρεις οτι κάτι μπορεί να πάει "στραβά" (ή τέλος πάντων, λιγότερο ευνοϊκά) και δεν προετοιμαστείς για αυτό....Τότε αυτό θα πάει στράβα (έστω και αν η πιθανότητα για αυτό το ενδεχόμενο φαινόταν πάρα πολύ μικρή)"....Αυτός...ξέρει!
Οπότε, ας δούμε λίγο πιο αναλυτικά αυτές τις δύο, φαινομενικά αθώες γραμμές της εισαγωγής, πρίν κάποιο ενδεχόμενο με πιθανότητα τόσο μικρή που δεν χωράει σε ανθρώπινο κεφάλι, αποφασίσει να καθυστερήσει αυτή τη σειρά πόστ για άλλη μια φορά (!).
Σύμφωνα λοιπόν με τα δεδομένα της Economist Intelligence Unit, οι δύο πόλεις στις οποίες ο τρόπος διαβίωσης απέχει τη "μεγαλύτερη απόσταση", είναι το Karachi - Pakistan και το Vancouver - Canada.
Εδώ βέβαια, δεν αναφερόμαστε στη γεωγραφική απόσταση, αλλά στην απόσταση όπως αυτή ορίζεται απο το διάνυσμα των 40 δεικτών που χαρακτηρίζουν κάθε πόλη. Αυτή η έννοια της απόστασης, έχει μια ιδιαίτερη σημασία και περιεχόμενο.
Για να δούμε λοιπόν: Τι πληροφορίες μπορεί να μας δώσει η έννοια της απόστασης; Ποιό είναι το μονοπάτι της "ελάχιστης προσπάθειας", ώστε το Karachi να "μετατραπεί" σε Vancouver; Ποιό είναι το μονοπάτι των λιγότερων μεταρυθμίσεων για τον ίδιο σκοπό; Ποιά είναι τα παραπάνω μονοπάτια όσο αφορά την Αθήνα;
Το κλειδί των απαντήσεων στις παραπάνω ερωτήσεις, βρίσκεται κατα ένα μεγάλο μέρος, στην έννοια της "απόστασης". Ήδη στο προηγούμενο κείμενο, είδαμε την έννοια της γνώριμης Ευκλείδιας απόστασης ανάμεσα στα σημεία ενός χώρου. Η μόνη διαφορά στη περίπτωση των δεδομένων της EIU και την "απόσταση" ανάμεσα σε δύο σημεία (για παράδειγμα, ανάμεσα στην Αθήνα και τη Θεσσαλονίκη) είναι οτι αυτός ο χώρος δεν έχει 3 αλλά 40 διαστάσεις.
Ένα χώρο 40 διαστάσεων, είναι ίσως δύσκολο να τον φανταστεί κανείς. Με τι μοιάζει ένα σπίτι στις 40 διαστάσεις; Με τι μοιάζει ένα αυτοκίνητο; Ένα ποτήρι, ή ένας απλός κύβος (ένα παραδοσιακά τρισδιάστατο σχήμα); Τι είναι διάσταση;
Διάσταση είναι μια ιδιότητα ενός αντικειμένου που αν τη στερηθεί, τότε δεν μπορεί να οριστεί πλήρως. Είναι αδύνατον να οριστεί ένας κύβος (ένα στερεό 3 διαστάσεων: Μήκος, Ύψος, Βάθος) στις 2 διαστάσεις γιατί θα ήταν αδύνατον να εκφραστεί το βάθος του.
Η απεικόνιση ενός πολυδιάστατου χώρου είναι απο τις λίγες περιπτώσεις όπου χρειάζεται να "δούμε" ακριβώς τη μορφή αυτού του χώρου. Συνήθως, τον δουλεύουμε "στα τυφλά" με βάση κάποιους απλούς κανόνες. Για παράδειγμα, με βάση τον απλό κανόνα: "Δύο διανύσματα είναι κάθετα όταν το εσωτερικό γινόμενο τους είναι 0", μπορούμε να κατασκευάσουμε κάθετα διανύσματα στις οποιεσδήποτε Ν διαστάσεις ΧΩΡΙΣ να χρειάζεται να τις "δούμε".....Δεν είναι ανάγκη να το "δείς" για να πιστείς (!) (Για περισσότερες λεπτομέρειες και μια ωραία εισαγωγή στο θέμα τουλάχιστον για τις 4 διαστάσεις μπορείτε να δείτε εδώ)
Δυστυχώς, δεν θα κατανοήσουμε ποτέ την μαγεία ενός "τετραπλού τόλουπ" στις 6 διαστάσεις (ο Κωστάλας παραμένει αδιάβλητος σε μετασχηματισμούς (!)), ή τι αδιανόητα αεροβατικά μπορεί να σκεφτεί ο πιλότος των 9 διαστάσεων. Δεν είμαστε φτιαγμένοι για αυτούς τους χώρους. Οι αισθήσεις μας είναι περιορισμένες στις 3 (το πολύ) διαστάσεις.
Στη προσπάθεια μας λοιπόν να κατανοήσουμε ένα 40διάστατο αντικείμενο στα περιθώρια ενός δισδιάστατου χώρου (ενός φύλου χαρτιού δηλαδή) και γνωρίζοντας πως δεν μπορούμε να του στερήσουμε καμία διάσταση τι κάνουμε;
Μπορεί να μην μπορούμε να στερήσουμε μια διάσταση απο τον κύβο, αλλά μπορούμε να βρούμε ένα τρόπο ώστε η τρίτη διάσταση να εκφραστεί μέσα απο τις δύο...Μπορούμε δηλαδή να προβάλουμε τις 3 διαστάσεις σε 2 ή γενικότερα, τις πολλές διαστάσεις σε λίγες...με την προυπόθεση βέβαια οτι αποδεχόμαστε κάποιο σφάλμα....Τι είναι αυτό το σφάλμα; Για να δούμε...
Στη παρακάτω εικόνα, ποιό σχήμα είναι ένα πραγματικό εξάγωνο και ποιό σχήμα είναι ένας κύβος καθώς τον κοιτάμε απο μια γωνία του;
Μαϊμού κύβοι! Κυκλοφορούν ανάμεσα μας!!!...
Οι τρείς γραμμές στο δεξιό σχήμα έχουν προστεθεί για να τονιστεί η ομοιότητα του εξαγώνου με τον κύβο απο αυτή τη γωνία...Ουσιαστικά πρόκειται για το ίδιο ακριβώς σχήμα.
Ακριβώς αυτό....Προσπαθόντας να προβάλουμε ένα κύβο απο τις τρείς στις δύο διαστάσεις, παραμορφώθηκε τόσο πολύ, που κατάντησε ένα τιποτένιο δισδιάστατο 6γωνο.....Απ' τα ανώγια, στα κατώγια...
Η προβολή των 3 διαστάσεων στις 2 είναι υπόθεση εύκολη...κυρίως επειδή τα μάτια και ο εγκέφαλος μας, είναι φτιαγμένα για να καταλαβαίνουμε δισδιάστατα αντικείμενα και να "φανταζόμαστε" τα τρισδιάστατα. Πώς όμως θα προβάλουμε 40 διαστάσεις; Δεν είναι μια δεν είναι δύο, δεν είναι τρείς....Είναι 40!
Είτε στη μια, είτε στις δύο, είτε στις τρείς, είτε στις δεκατρείς διαστάσεις, η έννοια της απόστασης* παραμένει η ίδια. Δέκα μέτρα απόσταση στις 20 διαστάσεις είναι ακριβώς δέκα μέτρα και στις 2 διαστάσεις. Και η απόσταση, είναι απλά ένας θετικός (πάντα) αριθμός.
Για να δούμε λοιπόν, μπορούμε να φανταστούμε ένα τρόπο, ώστε να προβάλουμε τα σημεία ενός 40διάστατου αντικειμένου στις 2 διαστάσεις με όσο το δυνατόν μικρότερη παραμόρφωση;
Η απάντηση σε αυτή την ερώτηση είναι σχετική με το αντικείμενο του διαγωνισμού Best City Contest. Ο διαγωνισμός μάλιστα, μας καλεί να προβάλουμε τις 40 διαστάσεις (ή υποσύνολο αυτών, ή ακόμα και νέο σύνολο με την προσθήκη άλλων δεικτών) σε 1. Να κατατάξουμε δηλαδή τις πόλεις επάνω σε μια γραμμή.
Αυτό μπορούμε να το κάνουμε με πάρα πολλούς τρόπους. Ένας απο αυτούς είναι η τεχνική του Multidimensional Scaling. Η τεχνική αυτή λύνει την εξής ωραία σπαζοκεφαλιά: Γνωρίζοντας μόνο τις αποστάσεις ανάμεσα σε ένα σύνολο απο σημεία σε κάποιο χώρο (Μ διαστάσεων), μπορείς να βρείς τη σχετική θέση των σημείων αυτών σε ένα άλλο χώρο (Ν διαστάσεων, Ν<=Μ), έστω και με κάποιο μικρό (κατα προτίμηση) σφάλμα;
Δεν μας ενδιαφέρει δηλαδή το πώς ακριβώς είναι τοποθετημένα αυτά τα σημεία πραγματικά στον 40διάστατο χώρο τους, αν δημιουργηθεί μια δισδιάστατη απεικόνιση που διατηρεί τις σχετικές αποστάσεις των σημείων τότε αντικρίζουμε ένα (απλό) χάρτη αυτού του (σύνθετου) πολυ-διάστατου τοπίου.
Να ένας "απλός" χάρτης:
Απο που πάνε για το Vancouver;;;;
Η παραπάνω εικόνα αποτελέι τη "λύση" της προβολής των 40 διαστάσεων σε 2 με τη μέθοδο του Multidimensional Scaling. Εδώ αξίζει να σημειωθεί οτι επειδή το πρόβλημα του ακριβούς ταιριάσματος των αποστάσεων ανάμεσα σε κάθε ζεύγος σημείων μπορεί να είναι αρκετά δύσκολο (ανάλογα με την εφαρμογή), μια υποκατηγορία μεθόδων του Multidimensional Scaling προσπαθεί απλά να "ταιριάξει" την κατάταξη των αποστάσεων παρά τις απόλυτες τιμές τους (Όπου εδώ η "κατάταξη" είναι η σειρά με την οποία εμφανίζονται οι πόλεις στα διαγράμματα του προηγούμενου κειμένου). Μια τέτοια μέθοδος έχει χρησιμοποιηθεί και για τη δημιουργία αυτού του χάρτη.
Μια πρώτη παρατήρηση είναι οτι οι πόλεις που ανήκουν σε εύρωστες οικονομικά χώρες (όπως η Ευρώπη, ο Καναδάς και η Αμερική) βρίσκονται όλες μαζί σε μια κοντινή γειτονιά ενώ οι πόλεις που βρίσκονται σε λιγότερο εύρωστες χώρες είναι πιο αραιά τοποθετημένες. Αυτό σημαίνει οτι ο τρόπος ζωής σε αυτές τις περιοχές έχει χαρακτηριστεί απο τους δείκτες και τη βαθμολόγηση της EIU, ώς περίπου ίδιος. Απο εκεί και περά όμως, οι υπόλοιπες πόλεις είναι λιγότερο προβλέψιμες και μπορεί να υπερτερούν σε μια μικρή ομάδα δεικτών αλλά να υστερούν σε κάποια άλλη.
Στο μεταξύ, γράφοντας κομμάτια αυτού του κειμένου, έληξε και η προθεσμία υποβολής συμμετοχών στον διαγωνισμό Best City Contest και είναι πλεόν δυνατόν να δούμε και την πολύ ενδιαφέρουσα δουλειά που έχει γίνει και απο άλλους χρήστες.
Έτσι λοιπόν, ένα παρόμοιο χάρτη στον οποίο είναι ακόμα πιο προφανής αυτή η διαίρεση δημιούργησε ο Alexander Kosenkov για τον διαγωνισμό και μπορείτε να τον δείτε στο BuzzData.
Η δημιουργία αυτού του χάρτη κάνει λίγο πιο προφανή πια και τα υπόλοιπα ερωτήματα, όπως: Πώς θα μπορούσε το Karachi να γίνει Vancouver; (και πόσο γρήγορα;) Ποιός είναι ο δρόμος της μικρότερης προσπάθειας ώστε με μικρούς μετασχηματισμούς ο τρόπος ζωής σε μια πόλη να προχωρήσει πρός αυτόν μιας άλλης πόλης;
Μικρές υποθέσεις και δοκιμές για τις απαντήσεις στις παραπάνω ερωτήσεις, με έκαναν να συμμετέχω τελικά και εγώ στον διαγωνισμό με ότι μπορούσα να καταφέρω στον διαθέσιμο ελεύθερο χρόνο και πάντα δουλεύοντας με την έννοια της απόστασης και προσπαθόντας να δημιουργήσω μια αντικειμενική κατάταξη (αντί για μια υποκειμενική που θα ήταν βασισμένη σε κάποια αυθαίρετη (ή και δικαιολογημένη) επιλογή δεικτών).
Οι ανυπόμονοι μπορείτε να ρίξετε μια ματιά στη συμμετοχή στο PDF που υπάρχει αναρτημένο στο BuzzData αν και σκοπεύω να γράψω μερικά ακόμα λόγια για τη συμμετοχή σύντ.........
Κάποια στιγμή στο μέλλον!
Σημειώσεις:
*: Η έννοια της απόστασης παραμένει η ίδια όταν ο χώρος συμμορφώνεται με την Ευκλείδια γεωμετρία....Υπάρχουν και γεωμετρίες στις οποίες η συντομότερη απόσταση ΔΕΝ είναι η ευθεία....Γίνεται, γίνεται....Θυμίσου, δεν είναι ανάγκη να το "δείς" για να "πειστείς"...





4 σχόλια:
Να σε δω να αναλύεις skylines μούμεινε, για να ξαναπώ πόσο μικρός είν' ο κόσμος.
Χμμμ...Μιλάς με γρίφους Stazybo :-) (Πότε είπες το πρώτο "Μικρός που είναι ο κόσμος"; )
Δεν είναι καθόλου άσχημη ιδέα όμως:
Αθήνα
Σόφια
Νέα Υόρκη
Λονδίνο
Σικάγο
Καράτσι (Περίπου)
Ο fillipolovato είχε μια σχετική ιδέα στην οποία χρησιμοπoίησε δεδομένα σχετικά με τη χωροταξία μιας πόλης που καθορίζει σε μεγάλο βαθμό τη ποιότητα ζωής.
Αποδείχτηκε γρίφος, επειδή αυτή τη φορά ο κόσμος παρέμεινε μεγάλος. Εγώ αναφερόμουν σε τέτοια skyline, που νομίζω είναι και η δική σου απάντηση στο πρόβλημα.
Και όχι, δεν εννοούσα ότι μ΄ εσένα έχει αποδειχτεί άλλη φορά πόσο μικρός είναι ο κόσμος.
Stazybo, σε ευχαριστώ πολύ για το contribution και συγγνώμη για την απογοήτευση :-)
Δημοσίευση σχολίου