Λόντρα, Παρίσι, Νιού Γιόρκ...

Λόντρα Παρίσι Νιού Γιόρκ Βουδαπέστη Βιέννη
μπρός την Αθήνα καμμιά σας καμμιά σας δε βγαίνει
γιατ' είναι πάντα γεμάτες με ρόδα οι ποδιές της
κι άσπρες δαντέλες τυλίγουν τις ακρογιαλιές της.

Λόντρα, Παρίσι, Αθήνα
Στίχοι: Μίμη Τραϊφόρου

 

Αυτά τραγουδούσε η Σοφία Βέμπο για την Αθήνα του 1944, λίγο πρίν το τέλος του Δευτέρου Παγκοσμίου Πολέμου και λίγο πριν την αρχή του δικού μας προσωπικού πολέμου, του εμφυλίου.

Πόσο όμως "απέχει" ο τρόπος ζωής στην Αθήνα σήμερα, απο τον τρόπο ζωής στο Παρίσι, τη Βουδαπέστη, τη Βιέννη και άλλες μεγάλες πόλεις το κόσμου; Ποιές δύο πόλεις βρίσκονται στα αντίποδα σημεία του τρόπου ζωής; Πώς μπορούμε να απεικονίσουμε τις διαφορές του τρόπου ζωής σε διάφορες πόλεις στον κόσμο σε μια εικόνα;

Τις απαντήσεις σε αυτές τις ερωτήσεις, μπορούν να μας δώσουν δύο σύνολα δεδομένων που δημοσιεύτηκαν πρόσφατα απο την Economist Intelligence Unit (EIU), στο BuzzData με αφορμή τον διαγωνισμό "Καλύτερη Πόλη Στον Κόσμο - 2012" (Best City In The World Contest - 2012).

Πολύ σύντομα, η EIU έχει ήδη δημιουργήσει ένα δείκτη διαβίωσης που κατατάσει τις πόλεις του κόσμου με βάση 39 παραμετρούς. Οι διαγωνιζόμενοι, καλούνται, με βάση αυτά τα δεδομένα, να δημιουργήσουν ένα νέο δείκτη του τρόπου ή της ποιότητας ζωής των πόλεων αυτών,  ο οποίος πιθανότατα να συμπεριλαμβάνει πρόσθετες παραμέτρους και δεδομένα που ο τρέχων δείκτης αγνοεί.
Για αυτό το λόγο, η EIU, δημοσιεύει μέσω του BuzzData δύο πολύ χρήσιμους πίνακες με διάφορους δείκτες διαβίωσης των πόλεων καθώς επίσης και του κόστους ζωής.


Τα δεδομένα ήταν πολύ ενδιαφέροντα και μια και δυό, εκτός διαγωνισμού, σκάρωσα μερικές απεικονίσεις που μπορείτε να βρείτε στο BuzzData. Γράφω αυτό το κείμενο για να πώ δύο λόγια παραπάνω για το τι δείχνουν αυτές οι απεικονίσεις αλλά και για να παρουσιάσω μια λίγο διαφορετική έκδοση τους.


Παραθέτω εδώ αμέσως τα γραφήματα, μαζί με κάποια πολύ σύντομα επεξηγηματικά σχόλια, ενώ περισσότερες λεπτομέρειες για την επεξεργασία μπορείτε να βρείτε στο τέλος του κειμένου....Όσο για την επιλογή των γραμματοσειρών και των χρωμάτων...Θα πώ ένα μόνο πράγμα:

"Greetings Professor Falken!"

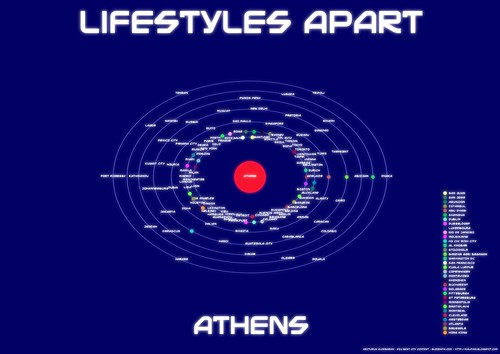
Η Αθήνα στον πιο συνηθισμένο της ρόλο, στο κέντρο της παγκόσμιας σκηνής (!)

(Όλες οι εικόνες έχουν δημιουργηθεί με αγνά υλικά και προέρχονται απο τη ψηφιακή φάρμα του ΑΑ)

Και ξεκινάμε με την Αθήνα και το γράφημα που ουσιαστικά ξεκίνησε αυτό το project. Εκ πρώτης όψεως βρίσκεται σε καλή γειτονιά. Την περιστοιχίζουν, σε κάποια απόσταση, πόλεις όπως το Λός Άντζελες, η Βοστώνη, η Βουδαπέστη και πολύ μακριά της η Τρίπολη, η Τεχεράνη και άλλες...Μας λείπει όμως εδώ, ένα μέτρο σύγκρισης...για να ξέρουμε τι εστί "κοντά" και τι "μακριά"...

   Η γειτονιά του Vancouver - Canada

Να και το μέτρο σύγκρισης! Το Vancouver ήταν μέχρι πολύ πρόσφατα η κορυφαία πόλη στη κατάταξη συνθηκών διαβίωσης της EIU αλλά έχασε απο τη Μελβούρνη. Το Vancouver, μαζί με το Karachi, στο Pakistan, έχουν τη μεγαλύτερη απόσταση σε ποιότητα ζωής (όπως περιγράφεται απο τους δείκτες της EIU).

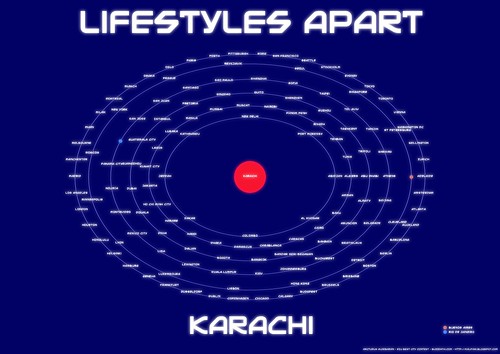
 Και απο το Vancouver, στην άλλη άκρη του κόσμου (και πιθανότατα και του τρόπου ζωής). Karachi - Pakistan

Ναι και το Karachi του οποίου η άμεση γειτονιά είναι το Κατμαντού, το Κολόμπο και το Δελχί...και μάλιστα σε αρκετή απόσταση...Το Karachi έχει τη χαμηλότερη βαθμολογία στους δείκτες διαβίωσης της EIU.

   Να και ένας...γεωγραφικός γείτονας... Sofia - Bulgaria

Μιά και μιλήσαμε για τα άκρα, ας αναφερθούμε και στο "μέσον". Ποιά πόλη δηλαδή είναι περίπου στο μέσο της απόστασης που ορίζεται απο το Vancouver και το Karachi? Και η πόλη αυτή είναι η Σόφια της γειτονικής Βουλγαρίας.


Προφανώς, μπορούμε να δημιουργήσουμε παρόμοιες εικόνες και για τις υπόλοιπες χώρες που περιγράφονται απο τα δεδομένα της EIU. Όμως μπορούμε, με μια πολύ όμορφη τεχνική, να φέρουμε όλες αυτές τις πόλεις και τις πληροφορίες για τις μεταξύ τους αποστάσεις σε μια και μόνο, δισδιάστατη εικόνα. Αυτό όμως θα το δούμε στο επόμενο κείμενο, πολύ σύντομα!



Για όσους έφτασαν ώς εδώ....και θέλουν να πάνε και παρακάτω....Ιδού τα ίνφοζ:

Τα Δεδομένα

Τα συγκεκριμένα δεδομένα που χρησιμοποιήθηκαν ήταν οι δείκτες διαβίωσης της EIU. Πρόκειται για μια σειρά απο 39 δείκτες για 140 πόλεις του κόσμου, ανάμεσα τους και η Αθήνα (για την οποία γίνεται ειδική αναφορά φέτος) που προσπαθούν να ποσοτικοποιήσουν διάφορες απόψεις της διαβίωσης στις πόλεις, όπως "Απειλή στρατιωτικής σύγκρουσης","Τρομοκρατική απειλή", "Διαθεσιμότητα εστιατορίων", "Ποιότητα παροχής ηλεκτρισμού", "Ποιότητα του οδικού δικτύου", "Επίπεδο λογοκρισίας" και άλλους δείκτες. Εδώ υπάρχει ένα λεπτό σημείο που αξίζει να αναφερθεί με μεγαλύτερη λεπτομέρεια: Οι δείκτες αυτοί, βρίσκονται όλοι στην ίδια κλίμακα με τιμές στο διάστημα [1..5] που ανταποκρίνονται στους χαρακτηρισμούς (Αποδεκτό, Ανεκτό, Ενοχλητικό, Ανεπιθύμητο, Απαράδεκτο) αντίστοιχα. Τις τιμές για κάθε πόλη, τις καθορίζει μια επιτροπή αναλυτών της EIU σε συνεργασία με τοπικούς αναλυτές απο την κάθε πόλη. Οι τιμές καθορίζονται σε σχέση με τη Νέα Υόρκη. Εδώ δεν θα μας απασχολήσει το πως ακριβώς γίνεται αυτή η μέτρηση ή αν η κλίμακα των 5 τιμών είναι αρκετή. Η εκτίμηση θεωρείται αντικειμενική και η κλίμακα αρκετή.

Το πολύ καλό στοιχείο που έχουν αυτά τα δεδομένα είναι ακριβώς αυτή η κοινή κλίμακα των 5 αριθμών γιατί αυτό σημαίνει οτι ορίζουν ένα ομοιόμορφο ορθογώνιο παραλληλεπίπεδο 39 - διαστάσεων. Με άλλα λόγια, αν ο κάθε δείκτης ήταν σε μια διαφορετική μονάδα και κλίμακα (για παράδειγμα, Ευρώ, χιλιόμετρα, ώρες, pascal) το παραλληλεπίπεδο δεν θα ήταν ομοιόμορφο και θα έπρεπε και πάλι να βρούμε ένα τρόπο να αντιστοιχίσουμε όλα τα δεδομένα σε ένα κοινό χώρο πρίν μπορούμε να κάνουμε τις οποιεσδήποτε συγκρίσεις.

Η Επεξεργασία

Η επεξεργασία των δεδομένων ήταν αρκετά απλή. Υπενθυμίζεται οτι ο πρωταρχικός σκοπός ήταν να εκτιμηθεί η απόσταση του τρόπου διαβίωσης ανάμεσα στην Αθήνα και τις άλλες πόλεις για τις οποίες υπήρχαν διαθέσιμα δεδομένα, ή πιο γενικά η απόσταση στον τρόπο διαβίωσης ανάμεσα σε οποιεσδήποτε δύο πόλεις. Το σύνολο των αριθμών για κάθε πόλη δημιουργούν ένα διάνυσμα 39 διαστάσεων.

Σκεφτείτε το αυτό, σαν ένα σημείο που θα μας έδινε το GPS, μόνο που απο αυτόν τον πλανήτη που μας έρχονται τα δεδομένα, κάθε σημείο του χώρου ορίζεται απο 39 αριθμούς αντί για τους συνηθισμένους 3 (Γεωγραφικό μήκος, πλάτος, Υψόμετρο) που μας δίνει το GPS επάνω στη Γή.

Ακριβώς με τον ίδιο τρόπο που μπορούμε να υπολογίσουμε την απόσταση μεταξύ δύο σημείων που περιγράφονται απο δυο τριάδες GPS αριθμών, υπολογίζουμε και την απόσταση ανάμεσα σε δυο διανύσματα 39 διαστάσεων. Η απόσταση αυτή είναι η συνηθισμένη Ευκλείδια απόσταση.

Υπολογίζοντας λοιπόν την απόσταση ανάμεσα στα διανύσματα όλων των ζευγών των πόλεων παίρνουμε ένα πίνακα γεμάτο αριθμούς που θα τον βαφτίσουμε "Πίνακα Αποστάσεων". Αυτός ο πίνακας έχει την εξής ωραία ιδιότητα. Επιλέγοντας μια γραμμή που αντιστοιχεί σε μια πολή, μπορεί να μας "μαρτυρήσει" τις αποστάσεις αυτής της πόλης και όλων των άλλων (σε κάθε στήλη της επιλεγμένης γραμμής).

Σκεφτείτε τον Πίνακα Αποστάσεων, σαν τους πίνακες που έχουν οι χάρτες μιας χώρας που δίνουν τις αποστάσεις ανάμεσα στις κυριότερες πόλεις.

Στη συνέχεια, χωρίζουμε τις αποστάσεις σε 10 ζώνες και μετράμε πόσες (και ποιές) πόλεις βρίσκονται στη κάθε ζώνη και απεικονίζουμε το αποτέλεσμα. Αυτό γίνεται με το λεγόμενο Ιστόγραμμα.

Σκεφτείτε το Ιστόγραμμα σαν τα αποτελέσματα των εκλογών, στον οριζόντιο άξονα βρίσκονται οι πολιτικές παρατάξεις και στον κάθετο ο αριθμός ψήφων. Στη δική μας περίπτωση, στον οριζόντιο άξονα βρίσκεται η "απόσταση" και στον κάθετο το πόσες (και ποιές) πόλεις βρίσκονται στη συγκεκριμένη απόσταση απο την εξεταζόμενη πόλη.

Τα Εργαλεία

Χρησιμοποιήθηκε η γλώσσα προγραμματισμού Python μαζί με τις "προσθήκες" Python - Cairo (για τα γραφικά και τις γραμματοσειρές) και την προσθήκη Python - Scipy για την επεξεργασία των αριθμών. Όλα αυτά τα εργαλεία (υψηλής ποιότητας) μαζί με την πλήρη τεκμηρίωση τους βρίσκονται σε ελεύθερη διάθεση. Οι γραμματοσειρές που χρησιμοποιήθηκαν ήταν η πολύ ενδιαφέρουσα (και καινούρια) Averia του Dan Sayers και η καταπληκτική Mainframe απο το Blambot, επίσης ελεύθερα διαθέσιμες. Το post-processing έγινε στο GIMP (πρόγραμμα επεξεργασίας εικόνας.....ναι.....και αυτό ελεύθερο).

Οι Απεικονίσεις

Δεν ήθελα απλά να δείξω μια σειρά απο ιστογράμματα και επειδή και τα δεδομένα μιλάνε για αποστάσεις, αποφάσισα να τα παραστήσω σαν το ηλιακό σύστημα, με την εξεταζόμενη πόλη στη μέση και τις υπόλοιπες πόλεις σαν δορυφόρους γύρω της. Μετά απο μια σειρά απο πειραματισμούς κατέληξα σε δύο πρότυπα που τα ονόμασα "Πάπυρος" (!) και "DEFCON" για προφανής (ελπίζω) λόγους. Το "Πάπυρος" είναι αυτό που εμφανίζεται στο BuzzData και εδώ παρουσιάστηκε το DEFCON.

Στα Όρια Της Ξενιτιάς...

Όπως ίσως καταλάβατε, το blog παρέμεινε «Παραμελημένο λόγο διακοπών». Ο ένας μήνας –περίπου- παραμονής στην Ελλάδα σήμαινε αρκετό χρόνο για βόλτες, φωτογραφίες –μικρά αναμνηστικά καθημερινότητας που κατα ένα περίεργο τρόπο περνάει απαρατήρητη-, σημειώσεις, βιβλία –που κούρνιαζαν καιρό τώρα, υπομονετικά, στο ράφι-, ύπνο –είδα όλα τα όνειρα που ανέβαλα όλο αυτό το καιρό λόγο δουλειάς-, φαϊ –έφαγα όλα τα φαγητά......τελεία, δε νοιώθω ιδιαίτερα υπερήφανος γι’ αυτό, λίγο φουσκωμένος μόνο- και Θάλασσα.....όχι απαραίτητα με αυτή τη σειρά...Προέχει η ασφάλεια.

Φωτογραφικά και συγγραφικά ντοκουμέντα θα ακολουθήσουν σύντομα. Πρός το παρόν όμως, ακολουθεί ένα κείμενο που παρά τη μικρή του έκταση γράφτηκε με κόπο απο το καναπέ, στο λεωφορείο, στο αεροδρόμιο και στο αεροπλάνο και το οποίο ξεχάστηκε αβίαστα μόλις πατήσαμε στο Ελ. Βενιζέλ και το ευλογημένο καλοκαίρι των 38 βαθμών.


Ένα ενδιαφέρον νοητικό πείραμα κινηματικής φυσικής ξεκινάει κάπως έτσι "Έστω οτι υπάρχει ένα πηγάδι / τούνελ που διαπερνά τη γή απο άκρο σε άκρο περνόντας απο το κέντρο της...".

Σε αυτό το post κάνω τα στραβά μάτια στους προφανείς λόγους γιατί κάτι τέτοιο είναι ακατόρθωτο -προς το παρόν (*)- και ρωτάω πολύ απλά "Που τελικά θα βγώ στην άλλη μεριά της Γής αν αρχήσω να σκάβω στον κήπο μου;". Διαλέξτε ένα καλό σημείο και αναρρωτηθείτε μαζί μου!

Το πείραμα, καταλήγει ρωτόντας "Τι κίνηση θα εκτελέσει ένα σώμα αν το ρίξουμε μέσα σε αυτό το πηγάδι;". Η απάντηση...φυσικά... είναι "Ταλάντωση". Υποθέτοντας οτι η Γή είναι μια απλή σφαίρα την οποία διαπερνά απο ένα σημείο στο ακριβώς απέναντι του ένα πηγάδι τότε πετώντας μέσα ένα αντικείμενο, αυτό θα εκτελέσει ομαλά επιταχυνόμενη κίνηση μέχρι το κέντρο της Γής (λόγο της βαρύτητας που θεωρείται οτι δρά πρός το κέντρο της σφαίρας) και μετά ομαλά επιβραδυνόμενη κίνηση μέχρι την επιφάνεια στο άλλο άκρο της απο όπου και κάποιος θα μπορούσε απλά να το αρπάξει τη στιγμή που η ταχύτητα του θα μηδενιζόταν. Αν υποτεθεί ακόμα οτι αυτό το τούνελ είναι κενό αέρος (και άρα δεν υπάρχουν τριβές), αυτό το σώμα θα συνεχίσει να ταλαντώνεται ανάμεσα σε αυτές τις δύο θέσεις για πάντα!

Η πλήρης ανάλυση δείχνει οτι το ταξίδι απο το ένα άκρο της Γής στο άλλο θα διαρκούσε περίπου 42 λεπτά (!) ενώ η μέγιστη ταχύτητα θα ήταν περίπου 28 χιλιάδες χιλιόμετρα ανα ώρα (Σχεδόν 23 φορές τη ταχύτητα του ήχου δηλαδή !!!).

Όλα ωραία και καλά ώς εδώ αλλά τι βρίσκεται ακριβώς στην άλλη μεριά της Γής απο μια οποιαδήποτε θέση?

Η απάντηση κρύβεται στα “Αντίποδα” Σημεία. Αυτά είναι τα εκ διαμέτρου αντίθετα σημεία επάνω στην υδρόγειο σφαίρα τα οποία και απέχουν τη μεγαλύτερη απόσταση που θα μπορούσε να μετρηθεί ποτέ ανάμεσα σε δύο σημεία επάνω στην επιφάνεια της Γής.

Για να βρείτε που ακριβώς είναι το σημείο στο οποίο πρέπει να σταθείτε για να καυχιέστε οτι φτάσατε «Στην άλλη άκρη της Γής» μπορείτε να χρησιμοποιήσετε το applet “Antipode Map” της Solution Realm Software. Όπως φαίνεται στο παρακάτω screenshot, αλλά όπως μπορείτε να διαπιστώσετε και μόνοι σας ακολουθόντας το link, όλη η επιφάνεια της Ελλάδας αντιστοιχεί κάπου στη μέση του πουθενά του Ειρηνικού Ωκεανού!

(Antipode Map, Η επιφάνεια της Ελλάδας αντιστοιχεί κάπου στον Ειρηνικό Ωκεανό....το οποίο μας δίνει μια πληροφορία για το μέγεθος....του Ειρηνικού)

Θεωρητικά λοιπόν, υπάρχει ένα όριο στη ξενιτιά ή τέλος πάντων, τό πόσο μακριά μπορεί κάποιος να βρεθεί απο το σπίτι του. Αυτό το όριο είναι η απόσταση ανάμεσα στα Αντίποδα σημεία που για το πλανήτη Γή είναι περίπου 20000 χιλιόμετρα.

Ένα βήμα πρός οποιαδήποτε κατεύθηνση απο αυτό το πουθενά του Ειρηνικού θα είναι πάντα ένα βήμα πιο κοντά στο σπίτι.




(*) Η βαθύτερη ανθρωπογεννής τρύπα που έχει σκαφτεί μέχρι σήμερα έχει βάθος περίπου 12 χιλιάδες μέτρα. Ονομάζεται η τρύπα του Kola και ήταν μέρος ενός επιστημονικού προγράμματος της -κάποτε- Σοβιετικής Ένωσης. Η διάτρηση διήρκεσε απο το 1970 μέχρι το 1989 οπότε και διεκόπει το πρόγραμμα λόγο απροσδόκητων θερμοκρασιών.
Το πείραμα είχε θέσει ώς απόλυτο στόχο το βάθος των 15 χιλιομέτρων όπου και αναμενόταν η οριακή για τη λειτουργία του τρυπανιού θερμοκρασία των 300 βαθμών της κλίμακας Celsius. Σε αυτό το επίπεδο το τρυπάνι θα είχε διανύσει τη μισή απόσταση απο το υπολογισμένο πάχος του μανδύα της Γής που είναι περίπου 30 χιλιόμετρα.

Παρ' όλα αυτά, είμαι σίγουρος οτι όταν "το αποφασίσουμε" ένα διαμπερές πηγάδι θα είναι απλά θέμα χρόνου.